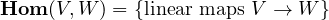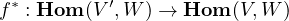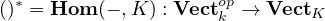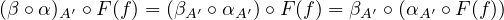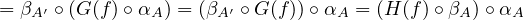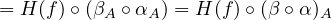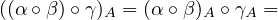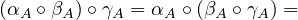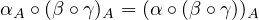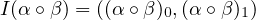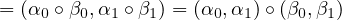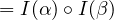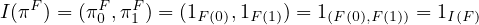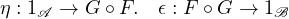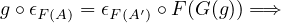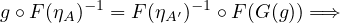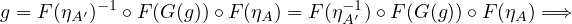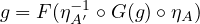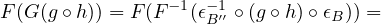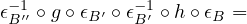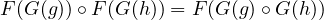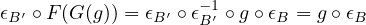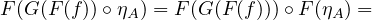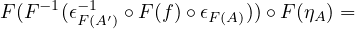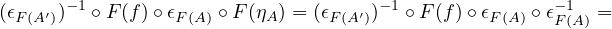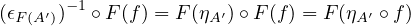1 Introduction

For me, the best way to learn something is to do it by explaining it to other people. With this in mind, I decided to make a website which supports blog posts so that I can document what I’m learning about. So you’ll be pretty much learning together with me. One of the things I was really excited about learning was category theory.

My motivation for that is the use of category theory in machine learning. Maybe I’ll do some category theory notes on machine learning later.

I’ll be using Tom Leinster’s book “Basic Category Theory” (available at https://arxiv.org/pdf/1612.09375) as a guide, and I’ll be following it closely. I’ll also try to introduce some of my own ideas/some stuﬀ I ﬁnd online.

For now, I’ll only put the statements of some theorems/lemmas/exercises. This is more of a reference for me. Treat this material as a draft. I’ll be updating it as I learn more. Also, it is more of a summary of the subject than actual detailed notes.

So without further ado, let’s begin.

1.1 Why study category theory?

From a pure mathematics point of view, category theory is a unifying theory. It provides a common language for discussing problems in diﬀerent branches of mathematics. It also provides a way to abstract away the details of a problem and focus on the essential structure of the problem.

It’s kind of a bird’s eye view of mathematics.

2 Categories

Deﬁnition 2.1. A category \(\cat{A}\) consists of:

1.: a collection \(\catobj{A}\) of objects;
2.: for each \(A, B \in \catobj{A}\), a collection \(\catmor{A}{A}{B}\) of maps or arrows or morphisms from \(A\) to \(B\);
3.: for each \(A, B, C \in \catobj{A}\), a function \begin{align*} \catmor{A}{B}{C} \times \catmor{A}{A}{B} & \to \catmor{A}{A}{C} \\ (f, g) & \mapsto f \circ g \end{align*}
called composition.
4.: for each \(A \in \catobj{A}\), an element \(1_A \in \catmor{A}{A}{A}\), called the identity on \(A\)

satisfying the following axioms:

1.: associativity: for each \(A, B, C, D \in \catobj{A}\) and each \(f \in \catmor{A}{C}{D}\), \(g \in \catmor{A}{B}{C}\) and \(h \in \catmor{A}{A}{B}\), \((f \circ g) \circ h = f \circ (g \circ h)\).
2.: identity laws: for each \(f \in \catmor{A}{A}{B}\), we have \(f \circ 1_A = f = 1_B \circ f\)

Example 2.2. The category \(\textbf{Set}\) has sets as objects and functions as morphisms. Composition is the usual composition of functions.

Example 2.3. The category \(\textbf{Grp}\) has groups as objects and group homomorphisms as morphisms. Composition is the usual composition of functions.

Example 2.4. The category \(\textbf{Top}\) has topological spaces as objects and continuous functions as morphisms. Composition is the usual composition of functions.

Example 2.5. The category \(\textbf{Vect}_K\) has vector spaces over a ﬁeld \(K\) as objects and linear maps as morphisms. Composition is the usual composition of functions.

Example 2.6. The category \(\textbf{Pos}\) has partially ordered sets as objects and order-preserving functions as morphisms. Composition is the usual composition of functions.

Example 2.7. The category \(\cat{C}\) whose objects are natural numbers and for each \(a \leq b \in \catobj{C}\), \(\catmor{C}{a}{b}\) contains exactly one element, namely the assertion that \(a \leq b\). We deﬁne the composition of assertions \(a \leq b\) and \(b \leq c\) as the assertion \(a \leq c\).

Remark 2.8. We can think of a group \(G\) as a category with one object and all elements of \(G\) as morphisms. The composition of morphisms is the group operation.

Deﬁnition 2.9. Every category \(\cat{A}\) has an opposite or dual category \(\cat{A}^{op}\), which has the same objects as \(\cat{A}\) but has \(\catmor{A^{op}}{A}{B} = \catmor{A}{B}{A}, \, \forall A, B \in \catobj{A}\) i.e. the arrows are reversed.

Deﬁnition 2.10. Given categories \(\cat{A}\) and \(\cat{B}\), there is a product category \(\cat{A} \times \cat{B}\), in which \begin{align*} \catobj{\cat{A} \times \cat{B}} & = \catobj{A} \times \catobj{B} \\ (\cat{A} \times \cat{B})((A, B), (A', B')) & = \catmor{A}{A}{A'} \times \catmor{B}{B}{B'} \end{align*}

Rigorously, this isn’t quite complete. You still need to deﬁne composition and identities. However, there is only one sensible way to do this here.

Proposition 2.11. A map in a category can have at most one inverse. That is, given a nonempty category \(\cat{A}\) and objects \(A, B \in \catobj{A}\), then for each \(f \in \catmor{A}{A}{B}\), there exists at most one \(g \in \catmor{A}{B}{A}\) such that \(f \circ g = 1_B\) and \(g \circ f = 1_A\).

Proof

Suppose \(g\) and \(g'\) are inverses of \(f\). Then \(g = g \circ 1_B = g \circ (f \circ g') = (g \circ f) \circ g' = 1_A \circ g' = g'\). \(\blacksquare \)

Deﬁnition 2.12. Let \(\cat{A}\) be a category and \(A, A' \in \cat{A}\). If there exists some morphism \(f \in \catmor{A}{A}{A'}\) s.t. \(f\) has an inverse \(g\), we say that \(f\) is an isomorphism from \(A\) to \(A'\). Moreover, we say that the objects \(A\) and \(A'\) are isomorphic and write \(A \cong A'\).

3 Functors

Deﬁnition 3.1. Let \(\cat{A}\) and \(\cat{B}\) be categories. A functor \(F : \cat{A} \to \cat{B}\) consists of:

1.

A function \(\catobj{A} \to \catobj{B}\) written as \(A \mapsto F(A)\)

2.

for each \(A, A' \in \catobj{A}\), a function \(\catmor{A}{A}{A'} \to \catmor{B}{F(A)}{F(A')}\) written as \(f \mapsto F(f)\), satisfying the following axioms

(a): For all \(A, B, C \in \catobj{A}\), \(f \in \catmor{A}{B}{C}\), \(g \in \catmor{A}{A}{B}\), \(F(f \circ g) = F(f) \circ F(g)\)
(b): For all \(A \in \catobj{A}\), \(F(1_A)=1_{F(A)}\)

Example 3.2. The identity functor preserves everything about the category. It’s not even fun to be considered.

Example 3.3. The easiest non trivial functors are the forgetful functors. There’s really no formal deﬁnition of this term, though. It’s just the name given to a functor which forgets some underlying structure. For example, the functor \(F : \textbf{Grp} \to \textbf{Set}\) which maps each group to its underlying set and each group homomorphism to its underlying function is a forgetful functor.

Deﬁnition 3.4. Let \(\cat{A}\) and \(\cat{B}\) be categories. A contravariant functor from \(\cat{A}\) to \(\cat{B}\) consists of:

1.

A function \(\catobj{A} \to \catobj{B}\) written as \(A \mapsto F(A)\)

2.

for each \(A, A' \in \catobj{A}\), a function \(\catmor{A}{A}{A'} \to \catmor{B}{F(A)}{F(A')}\) written as \(f \mapsto F(f)\), satisfying the following axioms

(a): For all \(A, B, C \in \catobj{A}\), \(f \in \catmor{A}{B}{C}\), \(g \in \catmor{A}{A}{B}\), \(F(f \circ g) = F(g) \circ F(f)\)
(b): For all \(A \in \catobj{A}\), \(F(1_A)=1_{F(A)}\)

i.e. the same as a normal (or covariant) functor from \(\cat{A}\) to \(\cat{B}\) except for the composition axiom, which is now inverted.

Remark 3.5. When we deﬁned functors and contravariant functors, all we said is that they ”consist of a list of things”. This allows us to regard a contravariant functor from \(\cat{A}\) to \(\cat{B}\) as simply a (covariant) functor from \(\cat{A}^{op}\) to \(\cat{B}\). Or even a functor from \(\cat{A}\) to \(\cat{B}^{op}\). I leave checking that this is indeed the case to the reader.

Example 3.6. Let \(K\) be a ﬁeld. For any two vector spaces \(V\) and \(W\) over \(K\), there is a vector space

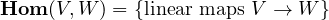
Hom (V,W ) = {linear maps V → W }

Fixing \(W\), any linear map \(f : V \to V'\) induces a linear map

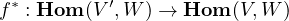
∗ ′ f : Hom (V ,W ) → Hom (V,W )

deﬁned at \(q \in \textbf{Hom}(V', W)\) by \(f^*(q) = q \circ f\). This deﬁnes a functor \(\textbf{Hom}(-, W) : \textbf{Vect}^{op}_K \to \textbf{Vect}_K\) i.e. a contravariant functor from the category of vector spaces over \(K\) to itself.

Indeed, given \(V \in \textbf{Vect}^{op}_K\), \(\textbf{Hom}(-, W)(V) = \textbf{Hom}(V, W) \in \textbf{Vect}_K\). Also, if \(f\) is a morphism in \(\textbf{Vect}^{op}_K\) from \(V'\) to \(V\) (i.e. a linear map from \(V\) to \(V'\)), then the aforementioned induced map \(f^{*}\) from \(\textbf{Hom}(V', W) \to \textbf{Hom}(V, W)\) is the morphism which is the output of the functor with input \(f\).

For completion, notice that the identity map \(f : V \to V\) corresponds to the induced map \(f^*\) which maps each \(q \in \textbf{Hom}(V, W)\) to \(q \circ f = q\) (i.e. the identity map on \(\textbf{Hom}(V, W)\)). Also, if \(f : V_1 \to V_2\), \(g : V_2 \to V_3\) are morphisms in \(\textbf{Vect}^{op}_K\), then we’re talking about the linear transformations \(f' : V_2 \to V_1\) and \(g' : V_3 \to V_2\). We have that \((g \circ f)' = f' \circ g' : V_3 \to V_1\). The induced map of this composition is the one which maps some \(q\) to \(q \circ f' \circ g'\). The induced maps to \(g'\) and \(f'\) are the ones that map \(q\) to \(q \circ g'\) and \(q \circ f'\), respectively. So the composition of these maps evaluated at \(q\) ﬁrst map \(q\) to \(q \circ f'\) and then to \(q \circ f' \circ g'\). So the composition law holds and we indeed have a functor.

Remark 3.7. If we set \(W=K\) (seen as a one dimensional vector space over itself) we get an important special case. We call \(\textbf{Hom}(V, K)\) the dual of \(V\) and is written as \(V^*\). So there is a contravariant functor

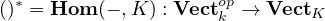
()∗ = Hom (− ,K) : Vectop→ VectK k

sending each vector space to its dual.

Deﬁnition 3.8. Let \(\cat{A}\) be a category. A presheaf on \(\cat{A}\) is a functor \(\cat{A}^{op} \to \textbf{Set}\) i.e. it’s a contravariant functor from \(\cat{A}\) to \(\textbf{Set}\).

Example 3.9. Let \(X\) be a topological space, and let \(\cat{O}(X)\) be the category whose objects are open sets of \(X\) and whose morphisms are inclusions. Then a presheaf on \(X\) is a contravariant functor \(F\) from \(\cat{O}(X)\) to \(\textbf{Set}\). We can deﬁne this functor in such a way that \(F(U) = \{\text{continuous functions } U \to \mathbb{R} \}\).

Notice that if \(U \subset V\) are open sets, then since there’s an unique morphism from \(U\) to \(V\) on \(\cat{O}(X)\), then there’s an unique morphism from \(F(V)\) to \(F(U)\). We can deﬁne this morphism as the restriction of functions.

Deﬁnition 3.10. A functor \(F : \cat{A} \to \cat{B}\) is faithful (resp. full) if for each \(A, A' \in \cat{A}\), the function \begin{align*} \catmor{A}{A}{A'} & \to \catmor{B}{F(A)}{F(A')} \\ f & \mapsto F(f) \end{align*}

is injective (resp. surjective).

Deﬁnition 3.11. Let \(\cat{A}\) be a category. A subcategory \(\cat{S}\) of \(\cat{A}\) is a category such that its objects \(\catobj{S}\) are a subclass of \(\catobj{A}\) and for each \(S, S' \in \catobj{S}\), \(\catmor{S}{S}{S'}\) is a subclass of \(\catmor{A}{S}{S'}\) which is closed under compositions and identities. It is a full subcategory if \(\catmor{S}{S}{S'} = \catmor{A}{S}{S'}\) for all \(S, S' \in \catobj{S}\).

Remark 3.12. A full subcategory can be speciﬁed only by specifying its elements. For example, \(\textbf{Ab}\) is a full subcategory of \(\textbf{Grp}\).

Proposition 3.13. Let \(\cat{S}\) be a subcategory of \(\cat{A}\). Then, the inclusion functor \(I : \cat{S} \to \cat{A}\) is faithful. Additionally, it’s full if and only if \(\cat{S}\) is a full subcategory of \(\cat{A}\).

Proof

Trivial. Let \(S, S' \in \catobj{S}\) and \(f_1, f_2 \in \catmor{S}{S}{S'}\). Then, \(I(f_1) = I(f_2) \implies f_1 = f_2\).

Additionally, suppose \(I\) is full. Then, \(I(\catmor{S}{S}{S'})=\catmor{A}{I(S)}{I(S')}=\catmor{A}{S}{S'}\). But \(I(\catmor{S}{S}{S'}) = \catmor{S}{S}{S'}\) since \(I\) is the inclusion map. Hence, \(\catmor{A}{S}{S'} = \catmor{S}{S}{S'}\), as desired.

Conversely, suppose \(\cat{S}\) is full. Then, \(I(\catmor{S}{S}{S'})=\catmor{S}{S}{S'}=\catmor{A}{S}{S'}=\catmor{A}{I(S)}{I(S')}\), which proves \(I\) is also full. \(\blacksquare \)

Remark 3.14. Let \(\cat{A}\) and \(\cat{B}\) be categories and let \(F : \cat{A} \to \cat{B}\) be a functor. Then, it is not necesssary that the image of \(F\) is a subcategory of \(\cat{B}\). Can you prove that by providing an example?

Proof

Suppose \(A, B, B', C \in \catobj{A}\) s.t. \(f \in \catmor{A}{A}{B}\), \(g \in \catmor{A}{B'}{C}\). Let \(X=F(A), Y=F(B)=F(B'), Z=F(C)\), \(p=F(f), q = F(g)\). Then \(p, q\) are in the image of \(F\) but \(q \circ p\) is not (necessarily).

\(\blacksquare \)

Proposition 3.15. Functors preserve isomorphisms. That is, if \(F:\cat{A} \to \cat{B}\) is a functor and \(A, B \in \catobj{A}\) s.t. \(A \cong B\), then \(F(A) \cong F(B)\).

Proof

From the isomorphisms, there exist \(f \in \catmor{A}{A}{B}, g \in \catmor{A}{B}{A}\) s.t. \(f \circ g = 1_A\) and \(g \circ f = 1_B\). Applying \(F\) at both sides of these equalities, we get \(F(f) \circ F(g) = 1_{F(A)}\) and \(F(g) \circ F(f) = 1_{F(B)}\) where \(F(f) \in \catmor{A}{F(A)}{F(B)}\) and \(F(g) \in \catmor{A}{F(B)}{F(A)}\). Hence, \(F(A) \cong F(B)\). \(\blacksquare \)

Exercise 3.16. Let \(A\) and \(B\) be preordered sets (i.e. a set with a preorder, which is a reﬂetive and transitive binary operation). Let \(\cat{A}\) and \(\cat{B}\) be the corresponding categories (i.e. the category whose elements are the elements of the preordered set and whose morphisms are the relations in the preorder).

Show that each functor \(F : \cat{A} \to \cat{B}\) corresponds to an order-preserving map \(f : A \to B\) are vice-versa.

Proof

Let \(F : \cat{A} \to \cat{B}\) be a functor. Deﬁne \(f\) as \(f(a)=F(a)\) (\(a \in A\)). Now, let \(a_1, a_2 \in A\) with \(a_1 \leq a_2\). Notice that \(a_1\) and \(a_2\) map to \(F(a_1)\) and \(F(a_2)\), respectively. Also, there’s an unique morphism from \(F(a_1)\) to \(F(a_2)\), namely \(F(a_1 \leq a_2)\). But by deﬁnition of \(\cat{B}\), if such a morphism exists, it its equal to the assertion that \(F(a_1) \leq F(a_2)\), which means that \(f(a_1) \leq f(a_2)\), which proves \(f\) is order-preserving.

Now, let \(f : A \to B\) be an order-preserving map. Deﬁne \(F\) as \(F(a)=f(a)\) (\(a \in A\)) and \(F(a_1 \leq a_2) = f(a_1) \leq f(a_2)\) (\(a_1, a_2 \in A\) s.t. \(a_1 \leq a_2\)). Clearly \(F\) is a functor. \(\blacksquare \)

Exercise 3.17. Is there a functor \(Z : \textbf{Grp} \to \textbf{Grp}\) with the property that \(Z(G)\) is the centre of \(G\) for each group \(G\)?

Proof

Well, yeah. Just take the image of a morphism between \(G\) and \(H\) to be simply it’s restriction to \(Z(G)\) if its an isomorphism (verify that the image of \(Z(G)\) is precisely \(Z(H)\) so we have an isomorphism between these two centres) and \(g \mapsto e_H\) otherwise. \(\blacksquare \)

Exercise 3.18. The composition of functors (deﬁned the obvious way) is a functor. Moreover, functor composition is associative.

Proof

Let \(\cat{A}, \cat{B}, \cat{C}, \cat{D}\) be categories, \(F : \cat{A} \to \cat{B}\), \(G : \cat{B} \to \cat{C}\), \(H : \cat{C} \to \cat{D}\) be functors.

For the composition, the obvious deﬁnition is so that \(G \circ F\) sends \(A \in \catobj{A}\) and a functor \(f\) in \(\cat{A}\) to \(G(F(A))\) and \(G(F(f))\), respectively. We need to prove that \(G \circ F\) satisﬁes the deﬁnition of a functor from \(\cat{A}\) to \(\cat{C}\).

For this, let \(A, A', A'' \in \catobj{A}\), \(f \in \catmor{A}{A'}{A''}\), \(g \in \catmor{A}{A}{A'}\). Now, \((G \circ F)(f \circ g) = G(F(f \circ g)) = G(F(f) \circ F(g)) = G(F(f)) \circ G(F(g))\) \(= (G \circ F)(f) \circ (G \circ F)(g)\).

Also, if \(A \in \catobj{A}\), we have \((G \circ F)(1_A) = G(F(1_A)) = G(1_{F(A)}) = 1_{G(F(A))} = 1_{(G \circ F)(A)}\). So \(G \circ F\) is a functor.

For the associativity, we just need to prove that the functors \((H \circ G) \circ F\) and \(H \circ (G \circ F)\) coincide at every object and morphism from \(\cat{A}\). But this is equivalent to proving the associativitiness of functions under composition, which we know it’s true. \(\blacksquare \)

Deﬁnition 3.19. We can form the category \(\textbf{CAT}\) of all categories. The objects of \(\textbf{CAT}\) are categories and the morphisms are functors. It’s trivial to see why this indeed forms a category.

Deﬁnition 3.20. Two categories are said to be isomorphic if they are isomorphic when seen as objects of \(\textbf{CAT}\).

4 Natural transformations

Deﬁnition 4.1. Let \(F, G : \cat{A} \to \cat{B}\) be functors. A natural transformation \(\alpha : F \to G\) is a family of morphisms \( \alpha _A \in \catmor{B}{F(A)}{G(A)}\) (\(A \in \catobj{A}\)) such that for each \(A, A' \in \catobj{A}\) and each \(f \in \catmor{A}{A}{A'}\), \(\alpha _{A'} \circ F(f) = G(f) \circ \alpha _A\). The maps \(\alpha _A\) are called the components of \(\alpha \).

Exercise 4.2. Let \(\cat{A}\) be a discrete category (whose morphisms are only the identities) and \(\cat{B}\) any category. Let \(F, G : \cat{A} \to \cat{B}\) be any functors. Show that for any family of morphisms \(\alpha _A \in \catmor{B}{F(A)}{G(A)}\), \(\alpha : F \to G\) is a natural transformation.

Proof

Let \(A, A' \in \catobj{A}\) and \(f \in \catmor{A}{A}{A'}\). Then, \(A=A'\) and \(f=1_{A}\). Thus, \(F(f)=1_{F(A)}\) and \(1_{G(A)}=G(f)\), so that \(\alpha _{A'} \circ F(f) = \alpha _{A'} \circ 1_{F(A)} = \alpha _{A'}\) \(= \alpha _{A} = 1_{G(A)} \circ \alpha _{A} = G(f) \circ \alpha _{A}\). \(\blacksquare \)

Example 4.3. Fix a positive integer \(n\). For any commutative ring \(R\), the matrices \(M_n(R)\) form a monoid. Moreover, any ring homomorphism \(R \to S\) induces a monoid homomorphism \(M_n(R) \to M_n(S)\). This deﬁnes a functor \(M_n : \textbf{CRing} \to \textbf{Mon}\) from the category of commutative rings to the category of monoids.

Also, the elements of any ring \(R\) form a monoid \(U(R)\) under multiplication, giving another functor \(U : \textbf{CRing} \to \textbf{Mon}\).

Now, every \(n \times n\) matrix \(X\) over a commutative ring \(R\) has determinant \(\det _R(X)\) i.e. each \(R\) gives a mapping \(\det _R : M_n(R) \to U(R)\).

Prove that \(\det : M_n \to U\) is a natural transformation.

Proof

Let \(R, R' \in \textbf{CRing}\) and let \(f : R \to R'\) be a ring homomorphism. Then, \(M_n(f)\) applies \(f\) entry-wise on a \(n \times n\) matrix and \(U(f)\) applies \(f\) to an element of \(U(R)\) when seen as an element of \(R\). Now, let \(M \in M_n(R)\).

Notice that when we apply \(det_{R'}\) to \(M_n(f)(M)\) when using thei Leibniz formula for the determinant, we can use the homomorphism properties of \(f\) ”in reverse” so that we have \(f\) of a sum of products. But this sum of products is the determinant of a matrix with entries in \(R\). More precisely, we get \(f(\det _R(M))\). But \(\det _R(M) \in R \subset U(R)\). So this can be seen as \(U(f)(\det _R(M))\).

So we have proved \(\det _{R'} \circ M_n(f) = U(f) \circ \det _R\). \(\blacksquare \)

Exercise 4.4. The composition of natural transformations is a natural transformation. More precisely, let \(\cat{A}, \cat{B}\) be categories \(F, G, H : \cat{A} \to \cat{B}\) be functors, and \(\alpha : F \to G\), \(\beta : G \to H\) be natural transformations. Then, \(\beta \circ \alpha : F \to H\) (deﬁned as \((\beta \circ \alpha )_A = \beta _A \circ \alpha _A\)) is a natural transformation.

Proof

Let \(A, A' \in \catobj{A}, f \in \catmor{A}{A}{A'}\). Then, using the associativiness of morphisms together with the facts that \(\alpha , \beta \) are natural transformations, we have:

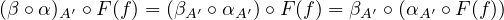
(β ∘α)A′ ∘ F(f) = (βA′ ∘ αA′)∘F (f ) = βA′ ∘(αA ′ ∘F(f))

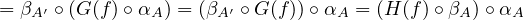
= βA′ ∘(G(f)∘ αA) = (βA′ ∘G(f))∘ αA = (H (f)∘βA )∘αA

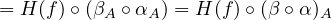
= H(f) ∘(β ∘ α ) = H (f)∘ (β ∘α ) A A A

\(\blacksquare \)

Exercise 4.5. Let \(\cat{A}\) and \(\cat{B}\) be categories. Construct (in a reasonable way) a category \(\cat{C}\) whose objects are functors from \(\cat{A}\) to \(\cat{B}\) and whose morphisms are the natural transformations. If you’ve constructed it correctly, then you ended up with what we call \([\cat{A}, \cat{B}]\) or \(\cat{B}^\cat{A}\).

Proof

Let \(F, G, H\) be objects of \(\cat{C}\), \(\alpha : G \to H\) and \(\beta : F \to G\) be natural transformtions. Then, \(\alpha \circ \beta \) was deﬁned previously and we proved it’s a natural transformation from \(F\) to \(H\).

For each functor (object of \(\cat{C}\)) \(F\), we deﬁne it’s identity morphism as the natural transformation \(\pi ^F : F \to F\) for which \(\pi ^F_A : F(A) \to F(A)\) is the identity morphism for every \(A\) i.e. \(\pi ^F_A = 1_{F(A)}\). (we need to check that this is indeed a natural transformation. For this, simply take \(A, A' \in \cat{A}\), \(f \in \catmor{A}{A}{A'}\). We have \(\pi ^F_{A'} \circ F(f) = 1_{F(A')} \circ F(f) = F(f) = F(f) \circ 1_{F(A)} = F(f) \circ \pi ^F_A\)).

Let \(F, G\) be objects of \(\cat{C}\) and \(\alpha : F \to G\) a natural transformation. Then, \(\alpha \circ \pi ^F\) is a natural transformation from \(F\) to \(G\). In particular, \((\alpha \circ \pi ^F)_A = \alpha _A \circ \pi ^F_A = \alpha _A \circ 1_{F(A)} = \alpha _A\). This means that \(\alpha \circ \pi ^F = \alpha \). Simmilarly, one can prove that if \(\beta : G \to F\) is a natural transformation, then \(\pi ^F \circ \beta = \beta \).

Finally, if \(F, G, H, I\) are objects of \(\cat{C}\), \(\alpha : H \to I\), \(\beta : G \to H\), \(\gamma : F \to G\) are natural transformations, then \((\alpha \circ \beta ) \circ \gamma \) and \(\alpha \circ (\beta \circ \gamma )\) are natural transformations from \(F\) to \(I\), but are they equal? To check equality, we just need to check if for each \(A \in \catobj{A}\), the morphisms they map to in \(\cat{B}\) coincide:

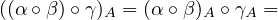
((α∘ β)∘γ )A = (α∘ β)A ∘ γA =

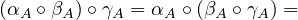
(α ∘β )∘γ = α ∘(β ∘γ ) = A A A A A A

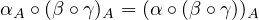
αA ∘(β ∘γ)A = (α∘ (β ∘γ))A

so they are indeed equal. \(\blacksquare \)

Example 4.6. Let \(2\) be the discrete category with two objects. Then, \([2, \cat{B}] \cong \cat{B} \times \cat{B}\).

Proof

The following \(I \in \textbf{Cat}([2, \cat{B}], \cat{B} \times \cat{B})\) is an isomorphism: \(I(F) = (F(0), F(1))\) where \(F\) is an object of \([2, \cat{B}]\) (and hence a functor from \(2\) to \(\cat{B}\)). Also, if \(\alpha \) is a morphism between objects of \([2, \cat{B}]\) (i.e. a natural transformation between functors \(F, G : 2 \to \cat{B}\)), we can map \(\alpha \) to \(I(\alpha ) = (\alpha _0, \alpha _1)\) where \(\alpha _0\) is the morphism from \(F(0)\) to \(G(0)\) and \(\alpha _1\) is the morphism from \(F(1)\) to \(G(1)\).

Now, \(I\) is clearly a morphism in \(\textbf{Cat}\), since it’s a functor from \([2, \cat{B}]\) to \(\cat{B} \times \cat{B}\). Indeed, let \(F, G, H \in [2, \cat{B}]\), \(\alpha : G \to H\), \(\beta : F \to G\). We have:

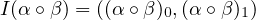
I(α ∘β) = ((α ∘β)0,(α ∘β )1)

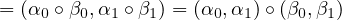
= (α ∘ β ,α ∘β ) = (α ,α ) ∘(β ,β ) 0 0 1 1 0 1 0 1

= I(α)∘ I(β)

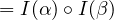
Also, if \(F \in [2, \cat{B}]\) and \(\pi ^F\) is the identity morphism, we have

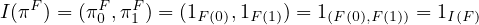
I(πF ) = (πF0 ,πF1 ) = (1F (0),1F (1)) = 1(F(0),F(1)) = 1I(F)

Now, let \(J \in \textbf{Cat}(\cat{B} \times \cat{B}, [2, \cat{B}])\) be deﬁned as: if \((B, C) \in \cat{B} \times \cat{B}\), \(J(B, C)\) is the functor which maps \(0\) to \(B\) and \(1\) to \(C\). Also, if \((\beta , \gamma )\) is a morphism between objects of \(\cat{B} \times \cat{B}\), \(J(\beta , \gamma )\) is the natural transformation which maps \(0\) to \(\beta \) and \(1\) to \(\gamma \). We can also prove that \(J\) is indeed a morphism in \(\textbf{Cat}\). But that’s too tedious. So we’ll jump straight to the part where we prove \(I\) and \(J\) are inverses.

Let \((B, C) \in \cat{B} \times \cat{B}\). Then, \((I \circ J)(B, C)=I(J(B, C))=(J(B, C)(0), J(B, C)(1)) =(B, C)\). Also, if \((f, g)\) is a morphism in \(\cat{B} \times \cat{B}\), then \((I \circ J)((f, g))=I(J(f, g))=(J(f, g)_0, J(f, g)_1) = (f, g)\). This means that the morphism \(I \circ J \in \textbf{Cat}(\cat{B} \times \cat{B}, \cat{B} \times \cat{B})\), which is a functor between this category, and itself coincides with the identity functor, so that \(I \circ J = 1_{\cat{\beta } \times \cat{\beta }}\).

Simmilarly, let \(F \in [2, \cat{B}]\). Then, \((J \circ I)(F)=J(I(F))=J(F(0), F(1))=J(F(0), F(1))=F\). Also, if \(\alpha \) is a morphism in \([2, \cat{B}]\), then \((J \circ I)(\alpha )=J(I(\alpha ))=J(\alpha _0, \alpha _1)=\alpha \). This means that \(J \circ I = 1_{[2, \cat{B}]}\).

\(\blacksquare \)

Deﬁnition 4.7. Let \(\cat{A}\) and \(\cat{B}\) be categories. A natural isomorphism between functors from \(\cat{A}\) to \(\cat{B}\) is an isomorphism in \([\cat{A}, \cat{B}]\). We say that these functors are naturally isomorphic and write \(F \cong G\).

Lemma 4.8. Let \(\cat{A}, \cat{B}\) be categories, \(F, G : \cat{A} \to \cat{B}\) be functors and \(\alpha : F \to G\) a natural transformation. Then \(\alpha \) is a natural isomorphism iﬀ \(\alpha _A : F(A) \to G(A)\) is an isomorphism for all \(A \in \cat{A}\).

Proof

Suppose \(\alpha \) is a natural isomorphism. Then, there exists a natural transformation \(\beta : G \to F\) such that \(\alpha \circ \beta = 1_G\) and \(\beta \circ \alpha = 1_F\).

Let \(A \in \cat{A}\) and \(\alpha _A : F(A) \to G(A)\). Then, \(\alpha _A \circ \beta _A = (\alpha \circ \beta )_A = (1_G)_A = 1_{G(A)}\). Simmilarly, one can prove \(\beta _A \circ \alpha _A = 1_{F(A)}\). Hence, \(\alpha _A\) is an isomorphism.

Now, suppose it’s an isomorphism for all \(A \in \cat{A}\). Deﬁne \(\beta : G \to F\) as the natural transformation suth that for all \(A \in \cat{A}\), \(\beta _A\) is the inverse of \(\alpha _A\).

We need to check that \(\beta \) is indeed a natural transformation. For this, take \(A, A' \in \cat{A}\) and \(f \in \catmor{A}{A}{A'}\).

Then, since \(\alpha \) is a natural transformation, we have \(\alpha _{A'} \circ F(f) = G(f) \circ \alpha _A\). Composing with \(\beta _A\) on the RHS and \(\beta _{A'}\) on the LHS we get

\begin{align*} \beta _{A'} \circ (\alpha _{A'} \circ F(f)) \circ \beta _A & = \beta _{A'} \circ (G(f) \circ \alpha _A) \circ \beta _A \\ (\beta _{A'} \circ \alpha _{A'}) \circ F(f) \circ \beta _A & = \beta _{A'} \circ G(f) \circ (\alpha _A \circ \beta _A) \\ 1_{F(A')} \circ F(f) \circ \beta _A & = \beta _{A'} \circ G(f) \circ 1_{G(A)} \\ F(f) \circ \beta _A & = \beta _{A'} \circ G(f) \end{align*}

Hence, \(\beta \) is a natural transformation, as desired.

Also, \((\alpha \circ \beta )_A = \alpha _A \circ \beta _A = 1_{G(A)}\). Simmilarly, \((\beta \circ \alpha )_A = 1_{F(A)}\). This means that \(\alpha \circ \beta = 1_G\) and \(\beta \circ \alpha = 1_F\). \(\blacksquare \)

Deﬁnition 4.9. Given functors \(F, G : \cat{A} \to \cat{B}\), we say that

\(F(A) \cong G(A)\) naturally in \(A\)

if \(F\) and \(G\) are naturally isomorphic.

The motivation for this alternative terminology is that if \(F(A) \cong G(A)\) naturally in \(A\), then \(F(A) \cong G(A)\) for all \(A \in \catobj{A}\). But more is true: we can choose isomorphisms \(\alpha _A : F(A) \to G(A)\) s.t. \(\alpha \) is a natural transformation.

Example 4.10. Let \(F, G\) be functors from a discrete category \(\cat{A}\) to \(\cat{B}\). Then, \(F \cong G\) iﬀ \(F(A) \cong G(A)\) for all \(A \in \cat{A}\)

Proof

Suppose \(F \cong G\). Then, \(\alpha \circ \beta = 1_G\) and \(\beta \circ \alpha = 1_F\) for some natural transformation \(\beta : G \to F \). Notice that \(\alpha _A : F(A) \to G(A)\) in an isomorphism with inverse \(\beta _A : G(A) \to F(A)\).

Now, suppose \(F(A) \cong G(A)\) for all \(A \in \cat{A}\). For each \(A\), let \(\alpha _A : F(A) \to G(A)\) be an isomorphism and \(\beta _A : G(A) \to F(A)\) its inverse. Then, \(\alpha \) and \(\beta \) are both natural transformations.

Indeed, let \(A, A' \in \catobj{A}\) and \(f \in \catmor{A}{A}{A'}\). Since \(\cat{A}\) is discrete, the non-emptiness of \(\catmor{A}{A}{A'}\) implies \(A=A'\), \(f=1_{A}\). This means that \(F(f)=1_{F(A)}\) and \(G(f)=1_{G(A)}\). So we have \(\alpha _{A'} \circ F(f) = \alpha _{A} \circ 1_{F(A)}\) \(= \alpha _A = 1_{G(A)} \circ \alpha _A = G(f) \circ \alpha _A\) so that \(\alpha \) is a natural transformation. One can prove that \(\beta \) is also a natural transformation. \(\blacksquare \)

Example 4.11. Let \(\textbf{FDVect}\) be the category of ﬁnite-dimensional vector spaces over some ﬁeld \(K\). The dual vector space construction on Remark 3.7 deﬁnes a contravariant functor from \(\textbf{FDVect}\) to itself.

We have two diﬀerent ways of treating a contravariant functor as a covariant one. Using both of these ways, the double dual functor \((-)^{**}\) is a (covariant) functor from \(\textbf{FDVect}\) to itself. Another functor from \(\textbf{FDVect}\) to itself is the identity one. It just so happens that there is a natural isomorphism between these two functors. Can you prove it?

Proof

Deﬁne the natural transformation \(\pi : 1_{\textbf{FDVect}} \to (-)^{**}\) as follows. For each \(V \in \textbf{FDVect}\), \(\pi _V\) is the morphism which takes some \(v \in V\) to the map which takes \(\varphi \in V^*\) to \(\varphi (v)\). Using standard linear algebra, we now that when we see \(\pi _V\) as a linear transformation, it’s isomorphic. Using this fact, it’s not hard to show that \(\pi \) is a natural transformation. Also, using lemma 4.8, we can prove that \(\pi \) is a natural isomorphism.

\(\blacksquare \)

Remark 4.12. By the language of deﬁnition 4.9, we can say that \(V \cong V^{**}\) naturally in \(V\).

This formalizes the idea that the double dual construction is a natural, or canonical one. You don’t need to choose anything to deﬁne it. It’s not just that we can deﬁne a linear isomorphism \(V \to V^{**}\) for each \(V\), but that we can do so in a way that respects the structure of the category of vector spaces. Although \(V^{*}\) is linearly isomorphic to \(V\), this isomorphism is not ”natural” at all. It depends on the choice of an arbitrary basis for \(V\).

The concept of natural isomorphism leads to another question. You see, we can think of two objects as ”the same” when there’s an isomorphism between them. We can think of functors as ”the same” when there’s a natural isomorphism between them. But when are categories ”the same”? Imposing that they must be isomorphic when seen as objects of \(\textbf{CAT}\) is unreasonably strict. This is because if \(\cat{A} \cong \cat{B}\), there exist functors \(F : \cat{A} \to \cat{B}\) and \(G : \cat{B} \to \cat{A}\) such that \(G \circ F = 1_{\cat{A}}\) and \(F \circ G = 1_{\cat{B}}\). But equality between functors is too strict, because, as I’ve just stated, the ideal notion of equality between functors should be natural isomorphism. This leads to the following deﬁnition

Deﬁnition 4.13. An equivalence between categories \(\cat{A}\) and \(\cat{B}\) consists of a pair of functors \(F : \cat{A} \to \cat{B}\) and \(G : \cat{B} \to \cat{A}\) together with natural isomorphisms

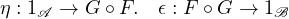
η : 1𝒜 → G ∘F. 𝜖 : F ∘ G → 1ℬ

If there exists an equivalence between \(\cat{A}\) and \(\cat{B}\), we say that \(\cat{A}\) and \(\cat{B}\) are equivalent, and write \(\cat{A} \simeq \cat{B}\). We also say that \(F\) and \(G\) are equivalencies.

Deﬁnition 4.14. A functor \(F : \cat{A} \to \cat{B}\) is essentially surjective on objects if for all \(B \in \cat{B}\), there exists \(A \in \cat{A}\) such that \(F(A) \cong B\).

Proposition 4.15. A functor is an equivalence if and only if it is full, faithfull and essentially surjective on objects.

Proof

Let \(F : \cat{A} \to \cat{B}\) be an equivalence. Then, there exists \(G : \cat{B} \to \cat{A}\) and natural isomorphisms \(\eta : 1_{\cat{A}} \to G \circ F\) and \(\epsilon : F \circ G \to 1_{\cat{B}}\). Then:

1.

\(F\) is full:

Let \(A, A' \in \catobj{A}\) and \(g \in \catmor{B}{F(A)}{F(A')}\). Then \(G(g) \in \catmor{A}{G(F(A))}{G(F(A'))}\). Also, \(\eta _A\) and \(\eta _{A'}\) are isomorphisms from \(A\) to \(G(F(A))\) and from \(A'\) to \(G(F(A'))\), respectively.

This means that \(F(\eta _A)\) and \(F(\eta _{A'})\) are isomorphisms from \(F(A)\) to \(F(G(F(A)))\) and from \(A'\) to \(F(G(F(A')))\), respectively. Moreover, \(\epsilon _{F(A)}\) and \(\epsilon _{F(A')}\) are isomorphisms from \(F(G(F(A)))\) to \(F(A)\) and from \(F(G(F(A')))\) to \(F(A')\), respectively. We’ve already proved that isomorphisms are unique. So we must have \(\epsilon _{F(A)} = F(\eta _A)^{-1}\) and \(\epsilon _{F(A')} = F(\eta _{A'})^{-1}\).

By the naturality of \(\epsilon \), we have

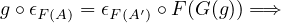
g∘𝜖F(A) = 𝜖F(A′) ∘F (G (g)) =⇒

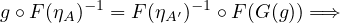
g∘ F(ηA)−1 = F (ηA′)−1 ∘F(G (g)) = ⇒

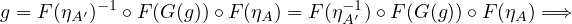
g = F (ηA ′)−1 ∘ F(G (g))∘ F(ηA) = F (η− 1′) ∘F (G (g))∘ F(ηA) = ⇒ A

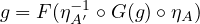−1 g = F (ηA ′ ∘G (g)∘ηA)

this means that we’ve found an \(f \in \catmor{A}{A}{A'}\) such that \(F(f) = g\), namely \(f = \eta _{A'}^{-1} \circ G(g) \circ \eta _{A}\).

2.

\(F\) is faithfull:

Let \(A, A' \in \catobj{A}\) and \(f_1, f_2 \in \catmor{A}{A}{A'}\) such that \(F(f_1) = F(f_2)\). Using the naturality of \(\eta \), we have \(G(F(h)) \circ \eta _A = \eta _{A'} \circ h\) for all \(h \in \catmor{A}{A}{A'}\). In particular, if \(h=f_i\), then, since \(\eta _{A'}\) is an isomorphism: \(f_i = \eta _{A'}^{-1} \circ G(F(f_i)) \circ \eta _A\). But the RHS is the same for \(i=1,2\), which means \(f_1 = f_2\).

3.

\(F\) is essentially surjective on objects:

Let \(B \in \catobj{B}\). Then, \(F(G(B)) \cong B\) by the isomorphism \(\epsilon _B\). So we’ve found an \(A \in \catobj{A}\) such that \(F(A) \cong B\), namely \(A=G(B)\).

Conversely, suppose that \(F\) if full, faithfull and essentially surjective on objects. We need to ﬁnd a functor \(G : \cat{B} \to \cat{A}\) and natural isomorphisms \(\eta : 1_{\cat{A}} \to G \circ F\) and \(\epsilon : F \circ G \to 1_{\cat{B}}\) to ﬁnish our proof.

Since \(F\) is essentially surjective on objects, for each \(B \in \cat{B}\), we can ﬁnd some \(A \in \cat{A}\) such that \(F(A) \cong B\). We can deﬁne \(G(B)\) to be this \(A\) (there may be multiple \(A\), but I don’t care). Trivially, \(F(G(B)) \cong B\) for all \(B \in \cat{B}\). Call this isomorphism from \(F(G(B))\) to \(B\) \(\epsilon _B\).

Also, for each \(B, B' \in \cat{B}\) and \(g \in \catmor{B}{B}{B'}\), consider the morphism \(\epsilon _{B'}^{-1} \circ g \circ \epsilon _B\). It is a morphism from \(F(G(B))\) to \(F(G(B'))\). Due to the faithfullness and fullness of \(F\) when applied to the map from \(\catmor{A}{G(B)}{G(B')}\) to \(\catmor{B}{F(G(B))}{F(G(B'))}\), we can ﬁnd a unique \(h \in \catmor{A}{G(B)}{G(B')}\) such that \(F(h) = \epsilon _{B'}^{-1} \circ g \circ \epsilon _B\). Deﬁne \(G(g) = h\). We can also write this as \(G(g) = F^{-1}(\epsilon _{B'}^{-1} \circ g \circ \epsilon _B)\). Then, \(G\) is a functor from \(\cat{B}\) to \(\cat{A}\).

Indeed, if \(B \in \cat{B}\), then \(G(1_B) = F^{-1}(\epsilon _B^{-1} \circ 1_B \circ \epsilon _B)\) \(= F^{-1}(1_{F(G(B))}) = 1_{G(B)}\). Also, if \(B, B', B'' \in \cat{B}\) and \(g \in \catmor{B}{B'}{B''}\), \(h \in \catmor{B'}{B}{B'}\), then

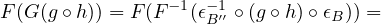
F (G(g∘ h)) = F(F −1(𝜖−B1′′ ∘(g∘ h)∘𝜖B)) =

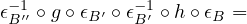
𝜖−B1′′ ∘ g∘𝜖B′ ∘ 𝜖−B1′ ∘h ∘𝜖B =

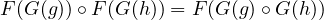
F (G (g))∘ F(G (h)) = F (G(g)∘G (h))

Since \(F\) is full and faithfull, we have \(G(g \circ h) = G(g) \circ G(h)\).

So \(G\) is indeed a functor. Also, \(\epsilon \) is a natural isomorphism. We’ve already checked that \(\epsilon _B\) is an isomorphism. Now it remains to check its naturality. Indeed, let \(B, B' \in \cat{B}\) and \(g \in \catmor{B}{B}{B'}\). Then, we have

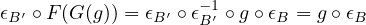
−1 𝜖B′ ∘F (G(g)) = 𝜖B′ ∘𝜖B′ ∘g∘ 𝜖B = g ∘𝜖B

Simmilarly, we can deﬁne \(\eta \) in the following way. Since \(\epsilon _{F(A)}^{-1}\) is an isomorphism from \(F(A)\) to \(F(G(F(A)))\), we can just take \(\eta _A = F^{-1}(\epsilon _{F(A)}^{-1})\). We have \(F(\eta _A \circ F^{-1}(\epsilon _{F(A)})) = \epsilon _{F(A)}^{-1} \circ \epsilon _{F(A)} = 1_{F(G(F(A)))}\) and \(F(F^{-1}(\epsilon _{F(A)}) \circ \eta _A) = \epsilon _{F(A)} \circ \epsilon _{F(A)}^{-1} = 1_{F(A)}\) so that \(\eta _A \circ F^{-1}(\epsilon _{F(A)}) = 1_{G(F(A))}\) and \(F^{-1}(\epsilon _{F(A)}) \circ \eta _A = 1_A\). This proves that \(\eta \) is an isomorphism.

Now, let \(A, A' \in \cat{A}\) and \(f \in \catmor{A}{A}{A'}\). Then,

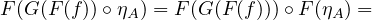
F(G (F (f)) ∘ηA) = F (G(F(f)))∘F (ηA ) =

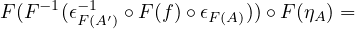
F(F− 1(𝜖−1 ′∘ F(f)∘ 𝜖 ))∘F (ηA) = F(A) F(A)

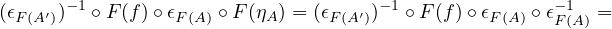
(𝜖F(A′))−1 ∘ F(f)∘𝜖F(A) ∘ F(ηA) = (𝜖F(A′))−1 ∘ F(f)∘𝜖F(A) ∘ 𝜖−F 1(A) =

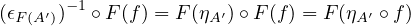
(𝜖 ′)−1 ∘F (f) = F(η ′)∘F (f ) = F(η ′ ∘ f) F (A ) A A

So the naturality of \(\eta \) follows from the fullness and faithfullness of \(F\). \(\blacksquare \)

Corollary 4.16. Let \(F : \cat{C} \to \cat{D}\) be a full and faithfull functor. Then \(\cat{C} \simeq \cat{C}'\), the subcategory of \(\cat{D}\) whose objects are isomorphic to \(F(C)\) for some \(C \in \cat{C}\).

Proof

By the deﬁnition of subcategory, one also needs to make explicit the subset of morphisms. When it is omitted, you may assume that it is equal to that of the ”super” category.

Let \(F' : \cat{C} \to \cat{C}'\) deﬁned by \(F'(C) = F(c)\), \(F'(f) = F(f)\). Then, \(F'\) is clearly a functor. Moreover, it is essentially surjective on objects. Since \(F'\) is additionally full and faithfull (which is inherited from \(F\)), then by the previous proposition, \(\cat{C} \simeq \cat{C}'\). \(\blacksquare \)

Example 4.17. Let \(\cat{A}\) be any category and \(\cat{B}\) a full subcategory of \(\cat{A}\) with at least one object from each isomorphism class of \(\cat{A}\). Then, the inclusion functor \(\cat{B} \to \cat{A}\) is full, faithfull and essentially surjective on objects. So \(\cat{B} \simeq \cat{A}\).

Example 4.18. Let \(\textbf{FinSet}\) denote the category of ﬁnite sets and functions between them. Let \(\cat{B}\) be a subcategory of it whose objects are \(\textbf{0}, \textbf{1}, \textbf{2}, \dots \) where \(\textbf{n}\) is an arbitrary chosen set with \(n\) elements. Then, by the previous example, \(\cat{B} \simeq \textbf{FinSet}\).

Exercise 4.19. Let \(\cat{C}\) be the subcategory of \(\textbf{CAT}\) whose objects are the categories with exactly one object. Then, \(\cat{C} \simeq \textbf{Mon}\).

Proof

Come on I won’t do everything for you. \(\blacksquare \)