Theorem 4.5 (Holder’s Inequality). If \(p, q \in [1, \infty ]\) with \(1/p + 1/q = 1\) then
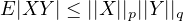
For me, the best way to learn something is to do it by explaining it to other people. With this in mind, I decided to make a website which supports blog posts so that I can document what I’m learning about. So you’ll be pretty much learning together with me. One of the things I was really excited about learning was measure theoretic probability.
If you’ve already had regular probability or statistics courses, you might be questioning if it is reasonable to study it all over again from the viewpoint of measure theory.
And you might be right. Maybe you really won’t need it. In fact, many statisticians don’t even use it. Depending on what you need to apply your probability or statistics knowledge to, there’s not a lot of things you’ll be missing out on if you don’t learn it.
So why does it even exist? Well, it’s just the natural way of formalizing probability theory. If you actually want to prove statements involving probability, then learning it from a measure theoretic viewpoint is the way to go.
For example, you might say that an event is “a collection of possible outcomes of a random experiment”. But this is too sloppy. There’s no actual mathematical framework behind it.
Another clear example are the convergence theorems. Measure theory helps defining lots of modes of convergence so that we know precisely what is being told when you say e.g. some random variable converges to another random variable.
TODO: show specific example of convergence
I’ll be using Rick Durrett’s book “Probability: Theory and Examples” as a guide, and I’ll be following it closely. I’ll also try to introduce some of my own ideas/some stuff I find online.
For now, I’ll only put the statements of some theorems/lemmas/exercises. This is more of a reference for me. Treat this material as a draft. I’ll be updating it as I learn more. Also, it is more of a summary of the book than actual detailed notes.
So without further ado, let’s begin.
Definition 2.1 (Probability Space). Let \(\Omega \) be a non-empty set, \(\mathcal{F}\) a \(\sigma \)-algebra on \(\Omega \) and \(P\) a measure on the measurable space \((\Omega , \mathcal{F})\) so that \(P(\Omega )=1\). We call the measure space \((\Omega , \mathcal{F}, P)\) a probability space.
It follows that the domain of \(P\) is \(\mathcal{F}\). So we are assigning each element of \(\mathcal{F}\) a value ranging from \(0\) to \(1\). In the ”naive” probability theory, we assign probabilities to events, so that in our more refined theory, the events are precisely the elements of \(\mathcal{F}\).
For this reason, \(\mathcal{F}\) is called the event space. The set \(\Omega \) is called the sample space and \(P\) is called the probability function.
We can say that the definition of a probability space is a mathematical construct that provides a formal model of a random process or experiment.
When an experiment is conducted, it results in exactly one outcome \(\omega \in \Omega \). All the events \(S\) in the event space \(\mathcal{F}\) that contain the selected outcome \(\omega \) are said to ”have occurred”. This means that when we model our probability space, the probability function \(P\) must be defined in a way that if the experiment were repeated arbitrarily many times, the number of occurrences of each event as a fraction of the total number of experiments, will (most likely) tend towards the probability assigned to that event.
Example 2.2 (Throw of a standard die). \(\Omega = \{1, 2, 3, 4, 5, 6\}\), \(\mathcal{F} = \mathcal{P}(\Omega )\) (i.e. the set of all subsets of \(\Omega \)) and \(P(\{ i \}) = 1/6\) for all \(i \in \Omega \). Notice that this indeed defines a probability space (i.e. \(\mathcal{F}\) is indeed a \(\sigma \)-algebra on \(\Omega \) and although I didn’t specify the value of \(P\) at all of \(\mathcal{F}\), it is clear that there exists a unique probability measure on \((\Omega , \mathcal{F})\) which satisfies what I specified, namely \(P(S) = |S|/6\), where \(|S|\) is the number of elements of some \(S \in \mathcal{F}\)).
Example 2.3 (Toss of a fair coin). Take \(\Omega = \{ \text{H}, \text{T} \}\), \(\mathcal{F} = \mathcal{P}(\Omega )\) and \(P\) so that \(P(\emptyset ) = 0\), \(P(\{ \text{H} \}) = 1/2\), \(P(\{ \text{T} \}) = 1/2\), and \(P(\{ \text{H}, \text{T} \}) = 1\).
Example 2.4 (Uniform distribution). Let \(\Omega = [0, 1]\), \(\mathcal{F} = \mathcal{B}_{\Omega }\) (i.e. the \(\sigma \)-algebra of Borel sets on \(\Omega \)) and \(P\) be the Borel measure on \([0, 1]\). In this case, for each \(a, b \in \Omega \) with \(a \leq b\), we have \(P((a, b)) = b - a\).
Definition 3.1 (Random element). A random element over a probability space \((\Omega , \mathcal{F}, P)\) is a measurable function \(X : (\Omega , \mathcal{F}) \to (S, \mathcal{S})\) where \((S, \mathcal{S})\) is an arbitrary measurable space. We say that the probability that \(X\) takes some value in \(T \in \mathcal{S}\) is \(P(X \in T) = P(\{\omega \in \Omega : X(\omega ) \in T \}) = P(X^{-1}(T))\) where the \(X \in T\) is just syntactic sugar for \(X^{-1}(T)\). In most cases, we’ll take \((S, \mathcal{S})\) to be \((\mathbb{R}, \mathcal{B}_{\mathbb{R}})\), in which case we’ll call \(X\) a random variable (or r.v.). If \((S, \mathcal{S}) = (\mathbb{R}^n, \mathcal{B}_{\mathbb{R}^n})\), we say \(X\) is a random vector.
Example 3.2 (Another throw of a die). Consider our previous throw of a standard die example. Let \(X\) be the function which maps each \(\omega \in \Omega \) to \(\omega \). Clearly, \(X\) is a measurable map from \((\Omega , \mathcal{F})\) to \((\mathbb{R}, \mathcal{B}_{\mathbb{R}})\) so that it is a random variable. Informally, this means that when we run our experiment, there is \(1/6\) chance of \(X\) being equal to \(i\) for each \(i \in \Omega \). Indeed, \(P(X=1) = P(X^{-1}(\{1\})) = P(\{1 \}) = 1/6\).
Notice the use of the notation \(P(X=1)\). If you want to be pedantic, you are right to say that we haven’t defined it properly. But don’t be like that. What I meant was clearly \(P(X \in \{1\})\) (which I’ve already defined). More precisely, whenever I have \(P\) of some expression involving random elements satisfying something on them, I mean the set of all \(\omega \in \Omega \) for which the expression involving the random element is true. Of course, we must verify that such a set is measurable, but that’s generally clear from the context.
Example 3.3 (Indicator function). Let \(A \in \mathcal{F}\). We define the indicator function \(\mathbf{1}_{A}\) of \(A\) from \(\Omega \) to \(\mathbb{R}\) as follows. If \(\omega \in A\), then \(\mathbf{1}_{A}(\omega ) = 1\). If this isn’t the case, \(\mathbf{1}_{A}(\omega ) = 0\). It is easy to check that \(\mathbf{1}_{A}\) is a r.v.
By the way, I’ll not bother being overly descriptive. For example, if I just say that \(X\) is a random element, you can immediately assume that what I mean is \(X : (\Omega , \mathcal{F}) \to (S, \mathcal{S})\) (because that’s the way I defined it).
Definition 3.4 (Distribution induced by a random element). Let \(X\) be a random element. Then, the function \(\mu : \mathcal{S} \to \mathbb{R}^+\) defined by \(\mu (A) = P(X \in A)\) is the distribution induced by \(X\). Notice how \(\mu \) is a measure over \((S, \mathcal{S})\).
Definition 3.5 (Distribution function induced by a random variable). Let \(X\) be a random variable. Then, we define its induced distribution function \(F : \mathbb{R} \to [0, 1]\) by \(F(x) = P(X \leq x)\).
Notice how we define both ”distribution” and ”distribution function” induced by a r.v. so be careful.
Theorem 3.6 (Properties of the distribution function). Any distribution function \(F\) has the following properties:
Proof
Theorem 3.7 (Existence of r.v. given distribution function). Let \(F : \mathbb{R} \to \mathbb{R}\) be a function satisfying all properties listed in the previous theorem. Then, there exists a probability space \((\Omega , \mathcal{F}, P)\) and a r.v. \(X\) over it such that the distribution function of \(X\) is precisely \(F\).
Proof
Remark 3.8. It may happen that \(F\) is not invertible. Even so, we shall write \(F^{-1}(x)\) meaning \(\sup \{ y \in \mathbb{R} : F(y) < x \}\) so that our \(X(\omega )\) on the proof above is \(F^{-1}(\omega )\).
Remark 3.9. Let \(X, Y\) be r.v.’s (when I mention multiple random elements, it’s implicit that they’re defined on the same probability space and have the same codomain). If the distribution of \(X\) is the same as the distribution of \(Y\) (which happens iff they have the same distribution function, due to the Lebesgue-Stieltjes theorem), we say \(X\) and \(Y\) are equal in distribution and write \(X \stackrel{d}{=} Y\).
Definition 3.10 (Density function). When the distribution function \(F\) can be written as \[ F(x) = \int \limits _{-\infty }^x f(t) dt \] we say that \(X\) has density function \(f\). In fact, we can start with an integrable function \(f\) satisfying \(f \geq 0\) and \(\int _{-\infty }^{\infty } f(t) dt = 1\).
Definition 3.11 (Discrete measure). A probability measure \(P\) is said to be discrete if there is a countable set \(S\) with \(P(S^c) = 0\).
Example 3.13 (Dense discontinuities). Although the set of discontinuities of \(F\) is countable, it may be dense. Indeed, let \(\{ q_n \}_{n=1}^\infty \) be an enumeration of the rationals and let \(\{ \alpha _n \}_{n=1}^\infty \) be a sequence of positive real numbers such that \(\sum _{n=1}^\infty \alpha _n = 1\). Define \[ F(x) = \sum \limits _{n=1}^\infty \alpha _n \cdot \mathbf{1}_{[q_n, \infty )}(x) \] then \(F\) is clearly a distribution function of some random variable \(X\).
Exercise 3.14. Let \((\Omega , \mathcal{F}, P)\) be a probability space and \(X\) be a r.v. over it with distribution function \(F\). Let \(Y = F \circ X\). Clearly \(Y\) is a r.v. Show that \(P(Y \leq y) = y\) for each \(y \in [0,1]\).
Definition 3.15. Let \(X\) be a random element. Then, \(\{ X^{-1}(B) : B \in \mathcal{S} \}\) is a \(\sigma \)-algebra. In fact, it is the smallest \(\sigma \)-algebra on \(\Omega \) that makes \(X\) measurable. We’ll call it the \(\sigma \)-algebra generated by \(X\) and denote it by \(\sigma (X)\).
Definition 3.16. It’s easy to see that \(\Omega _o = \{\omega : \lim \limits _{n \to \infty } X_n(\omega ) \text{ exists} \}\) is a measurable set.
If \(P(\Omega _o) = 1\), we say that \(X_n\) converges almost surely (a.s.).
Definition 4.2 (Expected Value). If \(X \geq 0\) is a r.v. then we define its expected value to be \(EX = \int X dP\), which may be \(\infty \). Clearly, if \(X^+\) and \(X^-\) are the positive and negative parts of \(X\) (\(X^+(\omega ) = \max (0, X(\omega ))\), \(X^-(\omega ) = \max (0, - X(\omega ))\)), respectively, then they are both r.v.’s. In this case, we define \(EX = E X^+ - E X^-\) and say it exists whenever the subtraction makes sense i.e. \(EX^+ < \infty \) or \(EX^- < \infty \).
\(EX\) is often called the mean of \(X\) and is denoted by \(\mu \). Notice that the expected value has all properties that integrals do
Proposition 4.3. Let \(X, Y \geq 0\) or \(E|X|, E|Y| < \infty \). Let \(a, b \in \mathbb{R}\).
Theorem 4.4 (Jensen’s Inequality). Suppose \(\varphi \) is convex. Then, \(E(\varphi (X)) \geq \varphi (EX)\).
Theorem 4.5 (Holder’s Inequality). If \(p, q \in [1, \infty ]\) with \(1/p + 1/q = 1\) then
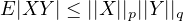
Theorem 4.7 (Chebyshev’s Inequality). Suppose \(\varphi : \mathbb{R} \to \mathbb{R}\) is a nonnegative measurable function, let \(A \in \mathcal{B}_{\mathbb{R}}\) and let \(i_A = \inf \{ \varphi (y) : y \in A \}\). Then
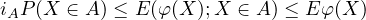
Remark 4.8. Some author’s call this Markov’s inequality and use the name Chebyshev’s inequality for the special case in which \(\varphi (x) = x^2\) and \(A = \{ x : |x| \geq a \}\):
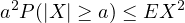
Theorem 4.11 (Dominated convergence theorem). If \(X_n \to X\) a.s. and \(|X_n| \leq Y\) a.s. for some \(Y\) with \(EY < \infty \) then \(EX_n \to EX\).
The special case in which \(Y\) is a constant is called the bounded convergence theorem.
Theorem 4.12 (Change of variables formula). Let \(X\) be a random element of \((S, \mathcal{S})\) with distribution \(\mu \), i.e., \(\mu (A) = P(X \in A)\). If \(f\) is a measurable function from \((S, \mathcal{S})\) to \((\mathbb{R}, \mathcal{B}_{\mathbb{R}})\) so that \(f \geq 0\) or \(E|f(X)| < \infty \), then
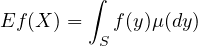
Definition 4.13 (Moments of r.v.’s and variance). If \(k\) is a positive integer, \(EX^k\) is called the \(k\)-th moment of \(X\). The first moment is called the mean. If \(EX^2 < \infty \) then the variance of \(X\) is defined to be \(\operatorname{var}(X) = E(X - EX)^2 = EX^2 - (EX)^2\).
From this, it’s immediate that \(\operatorname{var}(X) \leq EX^2\) and that if \(a, b \in \mathbb{R}\), \(\operatorname{var}(aX+b)=a^2 \operatorname{var}(X)\).